【kaggle】【quora insincere questions classification】1 模型融合
在实际机器学习应用中,亦或最近热门的数据科学竞赛中,掌握基本的集成方法是所有数据科学家都必备的一门绝杀技能,尤其是在大数据竞赛中,几乎所有的选手在最后阶段都会使用集成方法.
虽然集成方法并不是100%每次使用都会有很大的效果,但是从平时的比赛经验中,我们得到的一条结论是:集成方法在绝大多数情况下都会带来或多或少的帮助,而这在比赛中,尤其是最终成绩相差不大的情况下,集成的方法往往会成为取胜的关键之一.在不同类型的比赛中,我们也很难保证哪一种集成方法一定会比另外一种要好,评价的指标往往还得从线上的结果来看,只是说了解的集成方法越多一点,我们的胜率就会越高一些.
本篇notebook我们把集成方法分为两大类进行阐述,第一类从提交的文件进行集成(可以认为是预测结果的集成);第二类则是stacking/blending技术,每一类都会介绍一些非常有效实用的集成技术.
为什么集成方法有效
在信号编码的传输过程中,我们需要传输一堆01编码,但是传输的过程往往不会一帆风顺,有时会遇到一些干扰噪音,使得最终我们接收到的编码与我们当初传输的编码有一丝偏差,例如我们起初发送的编码为010101 但是我们最终接受到的编码可能为 010001,有一位编码出现了错误. 那么如何解决这个问题了? 一个简单的思路就是”集成”.
假设我们传输的真实信号编码为:
1110110011
我们将同一编码分三次进行发送,最终我们接受到的信号编码为:
①:1010110011 ②:1110110011 ③:1110110011
我们发现接收到的三个编码或多或少都出现了一点小小的问题,例如①中第二位编码的接收就出错了.但是②③次的接收第二位是对的,所以很容易地我们就想到:如果在多次不同的接收过程中,对于某一特定位置的编码,我们接收到的结果中10次有8次或者9次都为某一个值,那么我们就有很大的信心确定该位的值.(这个就是我们常说的投票机制的集成),而对于本问题,我们投票的结果就是:
1110110011
基本全部正确,在实际中,编码的传输只会在少数情况下出现错误,所以加上投票的机制,基本是可以保证最终的结果是99.9%的概率是没有问题的.集成方法是不是很有用?
提交结果的集成
- 投票集成(Voting ensemble)
- 算术平均数集成(Arithmetic mean based ensemble)
- 几何均值集成(Geometric mean based ensemble)
- 线上结果加权集成(Online scroe based ensemble)
- 排序均值集成(Rank averaging ensemble)
- log集成变种(log ensemble version2)
投票集成(Voting ensemble)
算法基本思路:
输入:多个不同分类器的分类结果 输出:最终的集成结果 基本步骤: 统计每个样本每个预测结果(常见于分类问题)出现的次数; 将每个样本出现的次数最多的那一个(众数)作为我们最终的集成结果.
from collections import defaultdict, Counter
from glob import glob
import sys
import re
glob_files = sys.argv[1]
loc_outfile = sys.argv[2]
weights_strategy = "uniform"
if len(sys.argv) == 4:
weights_strategy = sys.argv[3]
def kaggle_bag(glob_files, loc_outfile, method="average", weights="uniform"):
pattern = re.compile(r"(.)*_[w|W](\d*)_[.]*")
if method == "average":
scores = defaultdict(list)
with open(loc_outfile,"wb") as outfile:
#weight_list may be usefull using a different method
weight_list = [1]*len(glob(glob_files))
for i, glob_file in enumerate( glob(glob_files) ):
print("parsing:", glob_file)
if weights == "weighted":
weight = pattern.match(glob_file)
if weight and weight.group(2):
print("Using weight: ",int(weight.group(2)))
weight_list[i] = weight_list[i]*int(weight.group(2))
else:
print("Using weight: 1")
# sort glob_file by first column, ignoring the first line
lines = open(glob_file).readlines()
lines = [lines[0]] + sorted(lines[1:])
for e, line in enumerate( lines ):
if i == 0 and e == 0:
outfile.write(line)
if e > 0:
row = line.strip().split(",")
for l in range(1,weight_list[i]+1):
scores[(e,row[0])].append(row[1])
for j,k in sorted(scores):
outfile.write("%s,%s\n"%(k,Counter(scores[(j,k)]).most_common(1)[0][0]))
print("wrote to %s"%loc_outfile)
适用问题: 该方法常见于分类问题,Top-K推荐等预测结果是hard prediction的情况.
算术平均数集成(Arithmetic mean based ensemble)
算法基本思路: 输入:多个不同分类器的分类结果; 输出:最终的集成结果 基本步骤: 计算每个样本对应的所有结果的算术平均数,并将此每个样本的算术平均数作为我们最终的集成结果.
from collections import defaultdict
from glob import glob
import sys
glob_files = sys.argv[1]
loc_outfile = sys.argv[2]
def kaggle_bag(glob_files, loc_outfile, method="average", weights="uniform"):
if method == "average":
scores = defaultdict(float)
with open(loc_outfile,"wb") as outfile:
for i, glob_file in enumerate( glob(glob_files) ):
print("parsing:", glob_file)
# sort glob_file by first column, ignoring the first line
lines = open(glob_file).readlines()
lines = [lines[0]] + sorted(lines[1:])
for e, line in enumerate( lines ):
if i == 0 and e == 0:
outfile.write(line)
if e > 0:
row = line.strip().split(",")
scores[(e,row[0])] += float(row[1])
for j,k in sorted(scores):
outfile.write("%s,%f\n"%(k,scores[(j,k)]/(i+1)))
print("wrote to %s"%loc_outfile)
适用问题: 该方法常见于回归问题,分类问题中预测结果为概率的情况.
几何平均数集成(Geometric mean based ensemble)
基于几何平均数的集成方法在算法中使用的还不是很多,很多选手的分享都还是基于均值的较多,但是在实际情况中,有些时候基于几何平均数的效果要稍好于基于算术平均数的集成.
算法基本思路: 输入:多个不同分类器的分类结果; 输出:最终的集成结果 基本步骤: 计算每个样本对应的所有结果的几何平均数,并将每个样本的算术平均数作为我们最终的集成结果.
from __future__ import division
from collections import defaultdict
from glob import glob
import sysimport math
glob_files = sys.argv[1]
loc_outfile = sys.argv[2]
def kaggle_bag(glob_files, loc_outfile, method="average", weights="uniform"):
if method == "average":
scores = defaultdict(float)
with open(loc_outfile,"wb") as outfile:
for i, glob_file in enumerate( glob(glob_files) ):
print("parsing:", glob_file)
# sort glob_file by first column, ignoring the first line
lines = open(glob_file).readlines()
lines = [lines[0]] + sorted(lines[1:])
for e, line in enumerate( lines ):
if i == 0 and e == 0:
outfile.write(line)
if e > 0:
row = line.strip().split(",")
if scores[(e,row[0])] == 0:
scores[(e,row[0])] = 1
scores[(e,row[0])] *= float(row[1])
for j,k in sorted(scores):
outfile.write("%s,%f\n"%(k,math.pow(scores[(j,k)],1/(i+1))))
print("wrote to %s"%loc_outfile)
适用问题 该方法常见于回归问题,分类问题中预测结果为概率的情况.
线上结果加权集成(Online scroe based ensemble)
大家平时一直会说trust local CV,其实这是非常正确的一种做法,80%的实践中都是有效的,但是有一些情况却并非如此,有很多时序问题,变化非常快(而且不存在明显周期性),线上线下的分布可能差异较大,同时线上的测试集又是均匀采样的,那么这个时候拿线上作为验证集,也是一个选择.
线上结果加权集成的基本思路: 线上结果加权集成的方法也是实战中80%概率都会有效果的一种方法,该方法可以理解为一种拟合线上分布的方法.这种方法在数据竞赛这一块基本所有的老选手都会首选的方法之一.在实际工业生产中如果要使用这种方法的话,也可以通过线下验证集的结果进行加权.
算法基本思路: 输入:多个不同分类器的分类结果以及对应的线上成绩; 输出:最终的集成结果 基本步骤: 通过每个结果的线上成绩进行加权,线上分数高的权重就高,线上成绩相对低的权重就低,最终将加权的结果作为最终的结果(需保证所有的结果的 权重之和为1).
适用问题 该方法常见于回归问题,分类问题中预测结果为概率的情况.
排序均值集成(Rank averaging ensemble)
排序均值集成的基本思路: 排序均值集成的基本思路在很多AUC为指标的比赛中都取得了非常不错的成绩,使用相对顺序取代原先的概率值,例如: 我们预测某件事情发生的概率为:
0.30015,0.30011,0.30012
我们将其转化为对应的rank的值,这样更加能体现预测顺序的重要性.
3,1,2
算法思路: 输入:多个不同分类器的分类结果以及对应的线上成绩; 输出:最终的集成结果 基本步骤: 1.对每个分类器中分类的概率进行排序,然后用每个样本排序之后的得到的排名的值(rank)作为新的结果; 2.对每个分类器的rank的值求算术均值作为最终的结果
from __future__ import division
from collections import defaultdict
from glob import glob
import sys
glob_files = sys.argv[1]
loc_outfile = sys.argv[2]
def kaggle_bag(glob_files, loc_outfile):
with open(loc_outfile,"wb") as outfile:
all_ranks = defaultdict(list)
for i, glob_file in enumerate(glob(glob_files) ):
file_ranks = []
print("parsing:", glob_file)
# sort glob_file by first column, ignoring the first line
lines = open(glob_file).readlines()
lines = [lines[0]] + sorted(lines[1:])
for e, line in enumerate(lines):
if e == 0 and i == 0:
outfile.write(line)
elif e > 0:
r = line.strip().split(",")
file_ranks.append((float(r[1]), e, r[0]) )
for rank, item in enumerate(sorted(file_ranks) ):
all_ranks[(item[1],item[2])].append(rank)
average_ranks = []
for k in sorted(all_ranks):
average_ranks.append((sum(all_ranks[k])/len(all_ranks[k]),k))
ranked_ranks = []
for rank, k in enumerate(sorted(average_ranks)):
ranked_ranks.append((k[1][0],k[1][1],rank/(len(average_ranks)-1)))
for k in sorted(ranked_ranks):
outfile.write("%s,%s\n"%(k[1],k[2]))
print("wrote to %s"%loc_outfile)
适用问题 该方法常见于结果的评估指标与预测结果顺序有关问题,例如AUC等.
log集成变种(log ensemble version2)
这是一种很少有人知道的集成方法,效果亲测极佳。常见的问题是推荐问题,大家知道很多推荐问题是给用户推荐N个产品,然后再从N个产品计算有多少个产品被用户浏览或者点击来给与模型一定的评价,预测的N个产品有先后顺序,而且越在前面的产品的权重越大,也就是说第一个产品如果预测出错比第N个产品预测出错带来的loss更大。大家可能发现这个时候上面的所有方法都是可以用的,基于概率的基本都适用于这类问题。
但是有的时候可能数据可能比较大,这个时候大家没时间再去跑之前的model,但是我们手上有10份预测结果(非概率文件,而是每条记录都对应N个预测产品的结果文件),这个时候怎么样的集成方法能最有效呢?这个时候送大家一种神集成!
算法基本思路: 输入:M个分数类似的预测结果文件,没条记录对应N个预测结果; 输出:最终的输出N个预测结果 基本步骤: 1.统计每条记录中,每个推荐商品(N个商品)的出现位置,例如商品A,在第一份文件的推荐位置为1,在第二个文件的推荐位置是3,在第三个文件中未出现,此时我们计算商品A的得分为log1 + log3 + log(N+1),为出现我们用N+1表示; 2.找出所有没条记录中出现的产品的值并由小到大排序,取topN作为最终结果.
适用问题 该方法常见于推荐TopK的问题,尤其是TopK的顺序权重也不一样的问题.
Stacking/Blending
简单单层stacking方法(传统的方法Simple stacking with logistic regression/nonlinear algorithm)
这一块我们介绍stacking方法,也是我们比赛中尝试较多的方法.stacking背后的基本思路就是,使用一群基分类器(第一层),然后使用另外一个分类器(第二层)来组合前面第一层的预测结果,stacking的目的最直观的理解就是减小泛化误差.在1992年《STACKED GENERALIZATION》一文中还有一句关于Stacking的理解:
Stacked generalization can be seen as a more sophisticated version of cross-validation, exploiting a strategy more sophisticated than cross-validation’s crude winner-takes-all for combining the individual generalizers.
至于stacking在做什么,为什么有效,我们此处也直接引用University of Notre Dame的ensemble的ppt中的两句话进行阐述.
If a particular base-classifier incorrectly learned a certain region of the feature space, the second tier (meta) classifier may be able to detect this undesired behavior. Along with the learned behaviors of other classifiers, it can correct such improper training.
关于stacking与blending的区别:网上关于blending和stacking的说法有很多,很多时候大家已经把blending和stacking混为一谈,这边我们以台大林老师的课件作为参考,如果对细节感兴趣,建议大家去网上学习一下台大林老师相应的课程章节.此处我们以台大为主,把stacking当做是blending的一个特例,后续的介绍我们一律用stacking.

至于更深层次的理解和讨论,还是建议大伙查看相应文献和技术文档,此处不再详述,接下来,我们回归到我们的实际应用,着重介绍几种常见的stacking/blending技术.
- 简单单层stacking方法(传统的方法Simple stacking with logistic regression/nonlinear algorithm)
- 单层stacking方法(融入多项式特征)
- 两层stacking或者多层stacking
- stacking与其他技术的融合
简单单层stacking方法(传统的方法Simple stacking with logistic regression/nonlinear algorithm)
单层stacking方法基本思路
此处我们以两折(2-fold)stacking为例,N-fold stacking的思路类似:
2-fold stacking算法思路: 输入:训练集train,测试集test,m个第一层模型,1个第二层模型; 输出:最终的集成结果 基本步骤: 1.将训练集拆分为2部分:train_a,train_b,m个第一层模型,1个第二层模型; 2.对于第一层中的每一个模型model_1,model_2,…,model_m; 2.1 在train_a数据集合上面拟合第一层的模型并且对train_b做预测; 2.2.在train_b数据集合上面拟合第一层模型并且对train_a做预测; 2.3.将2.1,2.2中的结果进行合并获得一个新的特征train_level1_model_i; 2.4.在train数据集合上面拟合第一层模型并且对test做预测,获得新的特征test_level1_model_i 3.用第一层中获得的m个特征(train_level1_model_1,train_level1_model_2,…, train_level1_model_m)进行训练,再在新的测试集 (test_level1_model_1, test_level1_model_2, …, test_level1_model_m ) 上进行测试得到我们最终的提交结果;第二层通常会采用LR模型,不过很多非线性的模型例如XGB等等也都在一些比赛中取得了非常好的效果.
from sklearn import cross_validation
from sklearn.metrics import log_loss, accuracy_score
import numpy as np
import pandas as pd
import random
import md5
import json
def blend_proba(clf, X_train, y, X_test, nfolds=5, save_preds="",save_test_only="", seed=300373, save_params="", clf_name="XX", generalizers_params=[], minimal_loss=0,return_score=False, minimizer="log_loss"):
print("\nBlending with classifier:\n\t%s"%(clf))
folds = list(cross_validation.StratifiedKFold(y, nfolds,shuffle=True,random_state=seed)) print(X_train.shape)
dataset_blend_train = np.zeros((X_train.shape[0],np.unique(y).shape[0])) #iterate through train set and train - predict folds
loss = 0
for i, (train_index, test_index) in enumerate( folds ):
print("Train Fold %s/%s"%(i+1,nfolds))
fold_X_train = X_train[train_index]
fold_y_train = y[train_index]
fold_X_test = X_train[test_index]
fold_y_test = y[test_index]
clf.fit(fold_X_train, fold_y_train)
fold_preds = clf.predict_proba(fold_X_test)
print("Logistic loss: %s"%log_loss(fold_y_test,fold_preds))
dataset_blend_train[test_index] = fold_preds
if minimizer == "log_loss":
loss += log_loss(fold_y_test,fold_preds)
if minimizer == "accuracy":
fold_preds_a = np.argmax(fold_preds, axis=1)
loss += accuracy_score(fold_y_test,fold_preds_a)
#fold_preds = clf.predict(fold_X_test)
#loss += accuracy_score(fold_y_test,fold_preds)
if minimal_loss > 0 and loss > minimal_loss and i == 0:
return False, False
fold_preds = np.argmax(fold_preds, axis=1)
print("Accuracy: %s"%accuracy_score(fold_y_test,fold_preds)) avg_loss = loss / float(i+1)
print("\nAverage:\t%s\n"%avg_loss)
#predict test set (better to take average on all folds, but this is quicker)
print("Test Fold 1/1")
clf.fit(X_train, y)
dataset_blend_test = clf.predict_proba(X_test)
if clf_name == "XX":
clf_name = str(clf)[1:3]
if len(save_preds)>0:
id = md5.new("%s"%str(clf.get_params())).hexdigest()
print("storing meta predictions at: %s"%save_preds)
np.save("%s%s_%s_%s_train.npy"%(save_preds,clf_name,avg_loss,id),dataset_blend_train)
np.save("%s%s_%s_%s_test.npy"%(save_preds,clf_name,avg_loss,id),dataset_blend_test)
if len(save_test_only)>0:
id = md5.new("%s"%str(clf.get_params())).hexdigest()
print("storing meta predictions at: %s"%save_test_only)
dataset_blend_test = clf.predict(X_test)
np.savetxt("%s%s_%s_%s_test.txt"%(save_test_only,clf_name,avg_loss,id),dataset_blend_test)
d = {}
d["stacker"] = clf.get_params()
d["generalizers"] = generalizers_params
with open("%s%s_%s_%s_params.json"%(save_test_only,clf_name,avg_loss, id), 'wb') as f:
json.dump(d, f)
if len(save_params)>0:
id = md5.new("%s"%str(clf.get_params())).hexdigest()
d = {}
d["name"] = clf_name
d["params"] = { k:(v.get_params() if "\n" in str(v) or "<" in str(v) else v) for k,v in clf.get_params().items()}
d["generalizers"] = generalizers_params
with open("%s%s_%s_%s_params.json"%(save_params,clf_name,avg_loss, id), 'wb') as f:
json.dump(d, f)
if np.unique(y).shape[0] == 2:
# when binary classification only return positive class proba
if return_score:
return dataset_blend_train[:,1], dataset_blend_test[:,1], avg_loss
else:
return dataset_blend_train[:,1], dataset_blend_test[:,1]
else:
if return_score:
return dataset_blend_train, dataset_blend_test, avg_loss
else:
return dataset_blend_train, dataset_blend_test
适用问题 stacking方法基本适用于目前90%的问题,包括分类,回归,推荐等等.
单层stacking方法(融入多项式等特征)
2-fold stacking算法思路(融入多项式特征): 输入:训练集train,测试集test,m个第一层模型,1个第二层模型; 输出:最终的集成结果 基本步骤: 1. 将训练集拆分为2部分:train_a,train_b,m个第一层模型,1个第二层模型; 2. 对于第一层中的每一个模型model_1,model_2,…,model_m; 2.1. 在train_a数据集合上面拟合第一层的模型并且对train_b做预测; 2.2. 在train_b数据集合上面拟合第一层模型并且对train_a做预测; 2.3. 将2.1,2.2中的结果进行合并获得一个新的特征train_level1_model_i; 2.4. 在train数据集合上面拟合第一层模型并且对test做预测,获得新的特征test_level1_model_i 3. 用第一层中获得的m个特(train_level1_model_1,train_level1_model_2,…,train_level1_model_m)(对m个特征两两相乘(相除或者其他操作)形成新特征)行训练,再在新的测试集上(对m个测试集的特征进行与训练集相同的操作形成新的测试集特征)进行测试得到我们最终的提交结果: test_level1_model_1, test_level1_model_2, …, test_level1_model_m;
适用问题 此处的stacking方法算是3.2.1的一个简单扩展,所以同样适用于上述3.2.1中的所有问题,即分类,回归,推荐等等
两层stacking或者多层stacking
如果说3.2.2是在宽度上对传统stacking的一种扩展,那么本节要介绍的两层或多层stacking就是对传统stacking技术的一种深度上的扩展,一个直观的例子就是(下图摘自论文《Feature-Weighted Linear Stackingtwo-layer-stacking》):
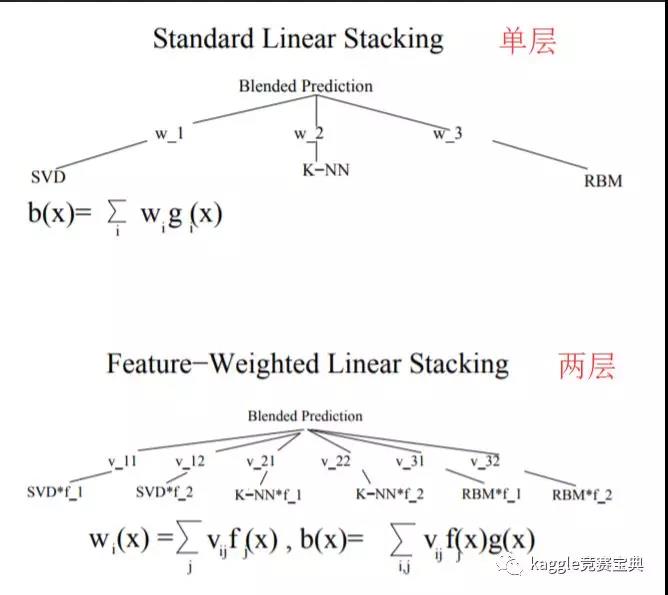
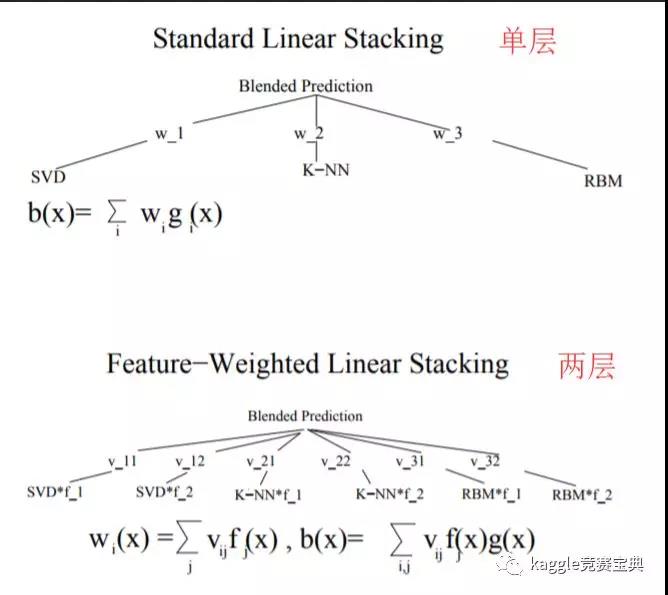 至于多层stacking的话就是继续在上面的基础上继续往后加层数,最新的中国机器学习界的大牛周老师的论文gcForest很多人也认为是一个改版的多层stacking.大家也可以关注一下.
至于多层stacking的话就是继续在上面的基础上继续往后加层数,最新的中国机器学习界的大牛周老师的论文gcForest很多人也认为是一个改版的多层stacking.大家也可以关注一下.
stacking与其他技术的融合
融入无监督特征
从上面的介绍中我们已经发现stacking的中间层是通过一堆model结果的输出来作为新的特征用作下一层的输入.既然如此,那么只要是有输出的model就都可以融入进来,所以我们在每一层就又可以加入一些无监督的方法,例如K-means以及其他各种聚类方法.
回归与分类的结合(Binning 技术)
确切地说,该部分属于一种特征工程的技巧,经常用于中间数据的处理,例如将预测概率为0-0.1设置为1,预测概率为0.1-0.5的设置为2等等.可以认为嵌在层间的特征工程(个人理解)……
参考资料
- 竞赛集成CookBook
- kaggle-ensembling-guide
- kaggle-ensembling-guide对应的代码Github
- Stacking slides
- Quora:What-is-stacking-in-machine-learning?
- Stacked generation
- Feature-Weighted Linear Stackingtwo-layer-stacking
- 林老师的课件
- ndemir关于Stacking的Github
- Introduction-to-ensembling-stacking-in-python
- How to Develop a Stacking Ensemble for Deep Learning Neural Networks in Python With Keras
Til next time,
gentlesnow
at 15:08

